Человек стоит на расстоянии от уличного фонаря

2016-04-02 21:46:15

Формулировка задачи: Человек, рост которого равен K м, стоит на расстоянии N м от уличного фонаря. При этом длина тени человека равна L м. Определите высоту фонаря (в метрах).

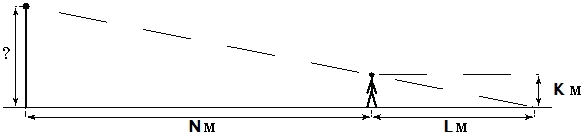
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 8 (Прикладная геометрия).

Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.

Пример задачи:

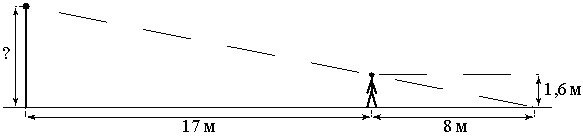
Человек, рост которого равен 1,6 м, стоит на расстоянии 17 м от уличного фонаря. При этом длина тени человека равна 8 м. Определите высоту фонаря (в метрах).

Решение:

Изобразим задачу с помощью геометрических фигур:

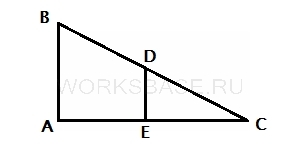
На картинке изображено 2 треугольника – малый и большой. Эти треугольники подобны по двум углам:

∠BAC = ∠DEC = 90°

∠BCA = ∠DCE – общий

Вычислим чему равен коэффициент подобия. Для этого возьмем две подобные стороны треугольников AC и EC и поделим большую на меньшую:

(17 + 8) / 8 = 3,125

Теперь можно вычислить высоту фонаря AB. Для этого нужно умножить рост человека DE на вычисленный коэффициент подобия:

1,6 ⋅ 3,125 = 5

Ответ: 5

В общем виде решение данной задачи выглядит следующим образом:

ВЫСОТА ФОНАРЯ = K ⋅ (N + L) / L

где K – рост человека, N – расстояние от человека до уличного фонаря, L – длина тени человека.

Осталось лишь подставить конкретные значения и получить ответ.

ЕГЭ база все задания ЕГЭ база задание 8

Поделитесь статьей с одноклассниками «Человек стоит на расстоянии от уличного фонаря – как решать».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.