Трёхзначное число при делении даёт остаток, если последнюю цифру числа перенести

Пример задачи:

Трёхзначное число при делении на 10 даёт в остатке 3. Если последнюю цифру числа перенести в начало его записи, то полученное число будет на 72 больше первоначального. Найдите исходное число.

Решение:

Для удобства назовем наше число abc, где каждая буква обозначает конкретный разряд числа: a – сотни, b – десятки и c – единицы. По условию задачи при делении на 10 числа в остатке получается 3. Это возможно только в одном случае: если число заканчивается на 3, то есть c = 3, а число на данный момент равно ab3.

Если перенесем последнюю цифру в начало, то получим число 3ab. Прибавим к числу ab3 число 72 столбиком и получим результат:

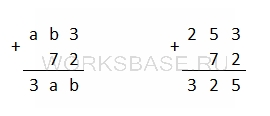
Цифры a и b вычисляются достаточно быстро. В разряде единиц к 3 прибавляем 2 и получаем, что b = 5. Заменяем все b в примере. В разряде десятков к найденному b прибавляем 7 и получаем 12. Таким образом, а = 2, а единица переходит в разряд сотен, так как разряд десятков переполнен. Заменили в примере все a и убедились что если к 2 прибавить единицу, которая перешла из разряда десятков, получится 3.

Таким образом, искомое число равно 253.

Ответ: 253