Равносторонний треугольник формулы
Равносторонний треугольник – это треугольник, у которого все стороны равны.
Другие виды треугольников:
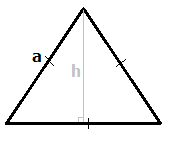
Любой равносторонний треугольник характеризуется стороной a (см. рисунок). При решении задач могут понадобиться высота h, радиусы вписанной (r) и описанной (R) окружности. Именно эти характеристики используются в формулах равностороннего треугольника при вычислении площади, периметра, а также радиусов вписанной и описанной окружностей.
Формула радиуса вписанной окружности для равностороннего треугольника
Радиус вписанной окружности r можно вычислить, зная сторону равностороннего треугольника:
r = a/(2√3)
Формула радиуса описанной окружности для равностороннего треугольника
Радиус описанной окружности R можно вычислить, зная сторону равностороннего треугольника:
R = a/(√3)
Формула периметра равностороннего треугольника
Периметр P равностороннего треугольника можно получить, зная его сторону:
P = 3a
Формулы площади равностороннего треугольника
p>При вычислении площади равностороннего треугольника можно использовать формулы, которые применяются для вычисления площади произвольного треугольника, так как равносторонний треугольник является частным случаем произвольного треугольника.Площадь равностороннего треугольника S можно вычислить, зная его сторону a:
S = (√3 ⋅ a2)/4
Площадь равностороннего треугольника S также можно вычислить, зная его высоту h:
S = h2/√3
Если в задаче присутствует окружность, вписанная в треугольник, площадь равностороннего треугольника можно вычислить через радиус окружности r:
S = 3√3 ⋅ r2
Если в задаче присутствует окружность, описанная вокруг треугольника, площадь равностороннего треугольника можно вычислить через радиус окружности R:
S = (3√3 ⋅ R2)/4
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.