На окружности отмечена точка С, отрезок АВ — диаметр окружности

2016-05-23 12:45:40

Формулировка задачи: На окружности радиуса R отмечена точка С. Отрезок АВ — диаметр окружности, дано AC. Найдите cos∠BAC.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 15 (Задачи по планиметрии).

Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.

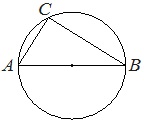
Пример задачи:

На окружности радиуса 5 отмечена точка С. Отрезок АВ — диаметр окружности, AC=6. Найдите cos∠BAC.

Решение:

Вписанный угол, опирающийся на диаметр окружности равен 90°. Следовательно, треугольник △ACB является прямоугольным.

AB – диаметр окружности, поэтому он равен:

AB = 2 ⋅ 5 = 10

Найдем cos∠BAC:

cos∠BAC = AC / AB = 6 / 10 = 0,6

Ответ: 0,6

В общем виде решение данной задачи по планиметрии выглядит следующим образом:

cos∠BAC = AC / (2R)

где R – радиус окружности.

Остается лишь подставить конкретные значения и подсчитать результат.

ЕГЭ база все задания ЕГЭ база задание 15

Поделитесь статьей с одноклассниками «На окружности отмечена точка С, отрезок АВ — диаметр окружности – как решать».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.