На окружности по разные стороны от диаметра AB взяты точки D и C
Формулировка задачи: На окружности по разные стороны от диаметра AB взяты точки D и C. Известен ∠DBA. Найдите угол DCB. Ответ дайте в градусах.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 15 (Задачи по планиметрии).
Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.
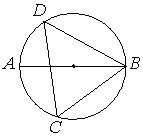
Пример задачи:
На окружности по разные стороны от диаметра AB взяты точки D и C. Известно, что ∠DBA=41°. Найдите угол DCB. Ответ дайте в градусах.
Решение:
Если внимательно изучить рисунок, можно заметить, что дуга ∪AD, на которую опирается вписанный угол ∠DBA, и дуга ∪BD, на которую опирается вписанный угол ∠DCB, в сумме составляют 180°, так как AB – это диаметр окружности.
Зная, что вписанный угол равен половине дуги, на которую он опирается, можно вычислить угол ∠DCB:
∪AD = 2 ⋅ ∠DBA = 82°
∪BD = 180° – ∪AD = 180° – 82° = 98°
∠DCB = 1/2 ⋅ ∪BD = 49°
Таким образом, угол ∠DCB равен 49°.
Ответ: 49
В общем виде решение данной задачи по планиметрии выглядит следующим образом:
∪AD = 2 ⋅ ∠DBA
∪BD = 180 – ∪AD = 180 – 2 ⋅ ∠DBA
∠DCB = 1/2 ⋅ ∪BD = 1/2 ⋅ (180 – 2 ⋅ ∠DBA)
Остается лишь подставить конкретные значения и подсчитать результат.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.
- Найдите высоту трапеции, если даны основания и боковая сторона
- В трапеции ABCD известно, что AB=CD, найдите угол ABD
- Около окружности описан многоугольник, найдите периметр
- Найдите радиус окружности вписанной в квадрат
- В окружности с центром O отрезки AC и BD — диаметры
- В треугольнике ABC дана сторона AC, BM - медиана, BH - высота
Есть другой способ решения?