В окружности с центром O отрезки AC и BD — диаметры
Формулировка задачи: В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен K°. Найдите угол ACB. Ответ дайте в градусах.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 15 (Задачи по планиметрии).
Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.
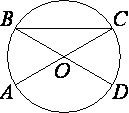
Пример задачи:
В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 124°. Найдите угол ACB. Ответ дайте в градусах.
Решение:
Диаметры AC и BD, пересекающиеся в точке O, образуют вертикальные углы. Поэтому:
∠BOC = ∠AOD = 124°
Рассмотрим треугольник BOC. Он является равнобедренным, поскольку OB и OC – радиусы окружности. А углы при основании равнобедренного треугольника равны:
∠OBC = ∠OCB = (180 – 124) / 2 = 28°
∠ACB = ∠OCB = 28°
Ответ: 28
В общем виде решение данной задачи по планиметрии выглядит следующим образом:
∠ACB = (180 – ∠AOD) / 2
Остается лишь подставить конкретные значения и подсчитать результат.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.
Есть другой способ решения?