Около окружности описан многоугольник, найдите периметр

2016-03-11 20:30:48

Формулировка задачи: Около окружности, радиус которой равен R, описан многоугольник, площадь которого равна S. Найдите его периметр.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 15 (Задачи по планиметрии).

Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.

Пример задачи:

Около окружности, радиус которой равен 3, описан многоугольник, площадь которого равна 33. Найдите его периметр.

Решение:

Для решения данной задачи соединим центр окружности со всеми вершинами многоугольника и проведем высоты в получившихся треугольниках к сторонам многоугольника.

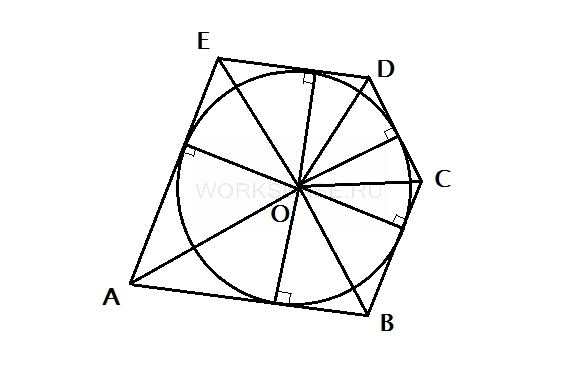
Чтобы получить площадь многоугольника, получим площади всех 5 треугольников и сложим их. При этом заметим, что высота каждого треугольника равна радиусу окружности.

S_△AOB = 1/2 ⋅ AB ⋅ R

S_△BOC = 1/2 ⋅ BC ⋅ R

S_△COD = 1/2 ⋅ CD ⋅ R

S_△DOE = 1/2 ⋅ DE ⋅ R

S_△EOA = 1/2 ⋅ EA ⋅ R

S_ABCDE = 1/2 ⋅ R ⋅ (AB + BC + CD + DE + EA)

Заметим, что в скобках получилась сумма длин всех сторон, то есть периметр P. Поэтому можно преобразовать площадь многоугольника в следующий вид:

S_ABCDE = 1/2 ⋅ R ⋅ P

Осталось подставить конкретные значения и выразить периметр:

33 = 1/2 ⋅ 3 ⋅ P

P = 33 / 3 ⋅ 2 = 22

Таким образом, периметр многоугольника равен 22.

Ответ: 22

В общем виде решение данной задачи по планиметрии выглядит следующим образом:

ПЕРИМЕТР МНОГОУГОЛЬНИКА = 2 ⋅ S / R

где S – площадь многоугольника, а R – радиус вписанной в него окружности.

Остается лишь подставить конкретные значения и подсчитать результат.

ЕГЭ база все задания ЕГЭ база задание 15

Поделитесь статьей с одноклассниками «Около окружности описан многоугольник, найдите периметр – как решать».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.