Сторона основания правильной треугольной пирамиды равна a

2017-11-05 16:45:30

Формулировка задания: Сторона основания правильной треугольной пирамиды равна a, а ее боковые грани наклонены к плоскости основания под углом β. Определить площадь боковой грани пирамиды.

Решение:

В правильной треугольной пирамиде в основании лежит равносторонний треугольник (ABC), а ее боковыми гранями являются 3 равных равнобедренных треугольника. Изобразим условие на картинке:

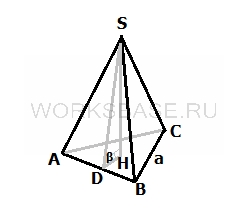
Для решения задачи нужно найти площадь одного из равнобедренных треугольников, пусть это будет △ASB. SH – высота пирамиды, DS – высота △ASB.

Рассмотрим △ABC, лежащий в основании пирамиды.

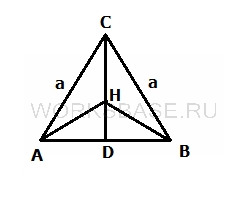
Он является равносторонним треугольником. Найдем в этом треугольнике DH, которая является радиусом вписанной окружности, по формуле:

DH = r = AB / (2√3) = a / (2√3)

Рассмотрим △DSH, который является прямоугольным:

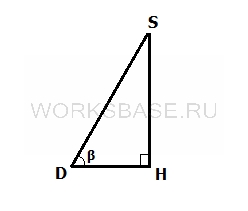
В нем нужно найти сторону DS, которая является гипотенузой прямоугольного треугольника. Найдем ее через косинус угла β:

cosβ = DH/DS

DS = DH/cosβ = a/(2√3) / cosβ = a / (2√3 ⋅ cosβ)

Рассмотрим △ASB, который является равнобедренным:

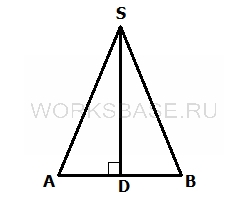
Найдем его площадь:

S_ASB = 1/2 ⋅ AB ⋅ DS = 1/2 ⋅ a ⋅ a / (2√3 ⋅ cosβ) = a² / (4√3 ⋅ cosβ)

Таким образом, площадь боковой грани пирамиды была найдена.

Ответ: a² / (4√3 ⋅ cosβ)

Поделитесь статьей с одноклассниками «Сторона основания правильной треугольной пирамиды равна a – решение и ответ».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.