В правильной четырехугольной пирамиде боковое ребро равно 10 см

2017-10-18 22:30:02

Формулировка задания: В правильной четырехугольной пирамиде боковое ребро равно 10 см. Найдите площадь боковой поверхности пирамиды, если апофема пирамиды равна 8 см.

Решение:

В правильной четырехугольной пирамиде в основании лежит квадрат (ABCD), а ее боковыми гранями являются 4 равных равнобедренных треугольника. Чтобы найти площадь боковой поверхности пирамиды, достаточно найти площадь одного равнобедренного треугольника (например, △ASB, где S – вершина пирамиды) и умножить ее на 4:

S_{бок.пов.} = 4 ⋅ S_ASB

Изобразим треугольник △ASB на рисунке:

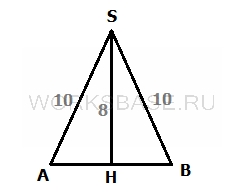
Апофема – это высота боковой грани, в данном случае это SH – высота равнобедренного треугольника.

Площадь треугольника △ASB равна:

S_ASB = 1/2 ⋅ AB ⋅ SH

Нужно найти сторону AB для вычисления площади. Заметим, что AH = BH так как △ASB равнобедренный (высота SH является медианой), поэтому достаточно найти AH и умножить на 2.

Рассмотрим треугольник △ASH. Так как SH – высота, треугольник △ASH прямоугольный. Найдем катет AH по теореме Пифагора:

AH = √SA² – SH² = √10² – 8² = √100 – 64 = √36 = 6

Значит сторона AB равна:

S_ASB = 2 ⋅ AH = 2 ⋅ 6 = 12

Площадь треугольника △ASB равна:

S_ASB = 1/2 ⋅ 12 ⋅ 8 = 48

А площадь боковой поверхности равна:

S_{бок.пов.} = 4 ⋅ 48 = 192

Ответ: 192

Поделитесь статьей с одноклассниками «В правильной четырехугольной пирамиде боковое ребро равно 10 см – решение и ответ».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.