В треугольнике ABC угол A равен 40°, угол B равен 20°, а AB-BC=4

2017-10-13 01:44:45

Формулировка задания: В треугольнике ABC угол A равен 40°, угол B равен 20°, а AB-BC=4. Найдите длину биссектрисы угла C.

Решение:

Изобразим треугольник на картинке:

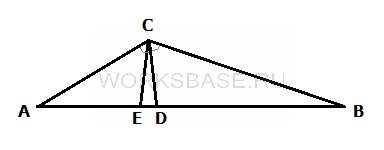
где CD – биссектриса угла C, которую нужно найти.

Для решения задачи нужны дополнительные построения. Добавим точку E, лежащую на AB, такую, чтобы:

EB = BC

то есть △ECB является равнобедренным. Рассмотрим этот треугольник. Угол ∠B в нем равен 20°, значит:

∠ECB = ∠CEB = (180° – 20°) / 2 = 80°

Рассмотрим треугольник △ACB. Углы ∠A и ∠B известны, значит:

∠C = 180° – 20° – 40° = 120°

А половина ∠C равна:

∠ACD = ∠BCD = 120°/2 = 60°

Рассмотрим треугольник △ACD. Углы ∠A и ∠ACD известны, значит:

∠ADC = 180° – 40° – 60° = 80°

Рассмотрим треугольник △ECD. Углы ∠CED (=∠CEB) и ∠CDE (=∠ADC) равны, значит треугольник является равнобедренным и:

EC = CD

∠ECD = 180° – 80° – 80° = 20°

Рассмотрим треугольник △ACE. Угол ∠A известен, угол ∠ACE можно получить как разницу углов ∠ACD и ∠ECD:

∠ACE = 60° – 20° = 40°

Заметим, что ∠ACE равен ∠A, то есть треугольник △ACE также равнобедренный:

AE = EC

Осталось вычислить искомую биссектрису CD:

CD = EC = AE = AB – EB = AB – BC = 4

Ответ: 4

Поделитесь статьей с одноклассниками «В треугольнике ABC угол A равен 40°, угол B равен 20°, а AB-BC=4».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.