Найдите высоту трапеции, если даны основания и боковая сторона

2016-05-16 18:50:50

Формулировка задачи: Основания равнобедренной трапеции равны a и b, боковая сторона равна c. Найдите высоту трапеции.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 15 (Задачи по планиметрии).

Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.

Пример задачи:

Основания равнобедренной трапеции равны 10 и 24, боковая сторона равна 25. Найдите высоту трапеции.

Решение:

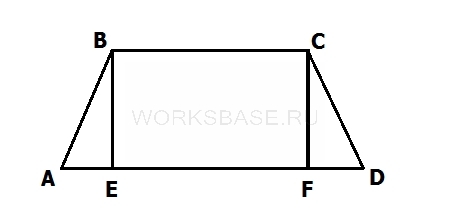
Рассмотрим равнобедренную трапецию ABCD, в котором нужно найти высоту BE:

BC = 10

AD = 24

AB = CD = 25

Для решения задачи можно перейти к прямоугольному треугольнику △ABE, в котором известна сторона AB и можно найти сторону AE:

AE = (AD – BC) / 2 = (24 – 10) / 2 = 7

Теперь можно найти катет BE по теореме Пифагора:

BE = √AB² – AE² = √25² – 7² = √576 = 24

Ответ: 24

В общем виде решение данной задачи по планиметрии выглядит следующим образом:

ВЫСОТА ТРАПЕЦИИ = √c² – ((b – a) / 2)²

где a – меньшее основание, b – большее основание, c – боковая сторона.

Остается лишь подставить конкретные значения и подсчитать результат.

ЕГЭ база все задания ЕГЭ база задание 15

Поделитесь статьей с одноклассниками «Найдите высоту трапеции, если даны основания и боковая сторона – как решать».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.