Укажите через запятую в порядке возрастания все основания систем счисления

2016-06-07 19:07:42

Формулировка задания: Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа A оканчивается на l.

Задание входит в ЕГЭ по информатике для 11 класса под номером 16 (Кодирование чисел. Системы счисления).

Рассмотрим, как решаются подобные задания на примерах.

Пример задания 1:

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 32 оканчивается на 4.

Решение:

Выполним перевод числа 32 из десятичной системы в систему N, которую нам нужно найти. Для этого поделим десятичное число на N, при этом остаток от первого деления будет равен 4:

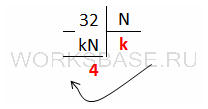
Было подобрано такое число k, что:

32 – kN = 4

kN = 28

Разложим число 28 на простые множители:

kN = 28 = 2 ⋅ 2 ⋅ 7

Осталось найти систему счисления N. При этом нужно учитывать, что N должно быть больше 4, иначе число в искомой системе счисления не сможет оканчиваться на 4:

N = 7 => k = 4, тогда 32₁₀ = 44₇

N = 14 => k = 2, тогда 32₁₀ = 24₁₄

N = 28 => k = 1, тогда 32₁₀ = 14₂₈

Таким образом, N может быть равно 7, 14 и 28.

Ответ: 7,14,28

Пример задания 2:

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 31 оканчивается на 11.

Решение:

Возьмем искомую систему счисления за N. Для решения задания нужно рассмотреть 2 случая:

31₁₀ = 11_N – число 31 в системе N равно 11
31₁₀ = ...11_N – число 31 в системе N заканчивается на 11 (перед 11 есть другие цифры)

Случай 1

Выполним перевод числа 31 из десятичной системы в систему N. При этом остаток от первого деления и его частное должны быть равны 1:

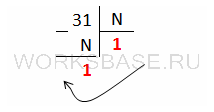
Получается, что:

31 – N = 1

N = 30

Значит, система счисления может иметь основание, равное 30.

Случай 2

Выполним перевод числа 31 из десятичной системы в систему N. При этом остатки от первого и второго деления равны 1:

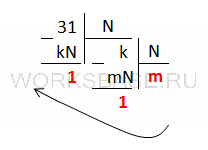
Были найдены такие положительные целые числа k и m, что:

31 – kN = 1
k – mN = 1

Выразим из второго равенства k:

k = mN + 1

И подставим его в первое равенство:

31 – N ⋅ (mN + 1) = 1

31 – mN² – N = 1

mN² + N – 30 = 0

Получили квадратное уравнение относительно N, если его решить, то будут получены основания систем счисления:

mN² + N – 30 = 0

a = m, b = 1, c = -30

D = 1² - 4 ⋅ m ⋅ (-30) = 1 + 120m

N1 = (-1 + √1 + 120m) / (2 ⋅ m)

N2 = (-1 – √1 + 120m) / (2 ⋅ m) < 0

В качестве ответа подойдет только первый корень, поскольку он положительный. Второй корень отрицательный, так как в числителе получится отрицательное число, а в знаменателе – положительное (m > 0).

Осталось подобрать такое число m, чтобы извлекался корень и в результате получилось натуральное число. Мы знаем, что m больше нуля, нужно ограничить это число сверху, чтобы сократить перебор.

Число m было получено после того, как исходное число 31 было дважды поделено на N с остатками. Значит:

m < 31 / N²

Про число N известно, что оно больше или равно 2 (иначе в данной системе счисления не может быть цифры 1). Поэтому чтобы получить максимально возможное значение дроби 31 / N², можно подставить в неравенство минимальное N = 2:

m < 31 / 2² = 31 / 4 = 7.75

Значит, нужно перебрать все целые числа от 1 до 7, проверить, извлекается ли корень и получается ли целый ответ:

m = 1:

N = (-1 + √1 + 120) / 2 = (-1 + 11) / 2 = 5

m = 2:

N = (-1 + √1 + 120 ⋅ 2) / (2 ⋅ 2) = (-1 + √241) / 4

корень не извлекается

m = 3:

N = (-1 + √1 + 120 ⋅ 3) / (2 ⋅ 3) = (-1 + √361) / 6 = (-1 + 19) / 6 = 3

m = 4:

N = (-1 + √1 + 120 ⋅ 4) / (2 ⋅ 4) = (-1 + √481) / 8

корень не извлекается

m = 5:

N = (-1 + √1 + 120 ⋅ 5) / (2 ⋅ 5) = (-1 + √601) / 10

корень не извлекается

m = 6:

N = (-1 + √1 + 120 ⋅ 6) / (2 ⋅ 6) = (-1 + √721) / 12

корень не извлекается

m = 7:

N = (-1 + √1 + 120 ⋅ 7) / (2 ⋅ 7) = (-1 + √841) / 14 = (-1 + 29) / 14 = 2

Таким образом, основаниями систем счисления могут быть числа 2, 3, 5 и 30.

Ответ: 2,3,5,30

ЕГЭ все задания ЕГЭ задание 16

Поделитесь статьей с одноклассниками «Укажите через запятую в порядке возрастания все основания систем счисления – как решать».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.