В некоторой системе счисления записи десятичных чисел заканчиваются

2016-06-07 17:40:44

Формулировка задания: В некоторой системе счисления записи десятичных чисел A и B заканчиваются на K. Определите основание системы счисления.

Задание входит в ЕГЭ по информатике для 11 класса под номером 16 (Кодирование чисел. Системы счисления).

Рассмотрим, как решаются подобные задания на примере.

Пример задания:

В некоторой системе счисления записи десятичных чисел 66 и 40 заканчиваются на 1. Определите основание системы счисления.

Решение:

Выполним перевод чисел 66 и 40 из десятичной системы в систему x. Для этого поделим каждое число на x, при этом остаток от первого деления должен быть равен 1, так как число в системе x должно заканчиваться на 1:

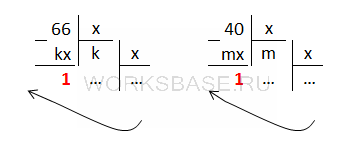
Были найдены такие числа k и m, что при вычитании в каждом случае получилась единица:

66 – kx = 1
40 – mx = 1

kx = 65
mx = 39

Разложим числа 65 и 39 на простые множители, чтобы найти их общий делитель, то есть число x:

65 = 5 ⋅ 13

39 = 3 ⋅ 13

Единственным общим множителем является число 13. Поэтому оно и является основанием системы счисления.

Выполним проверку:

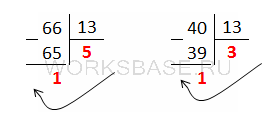
Ответ: 13

ЕГЭ все задания ЕГЭ задание 16

Поделитесь статьей с одноклассниками «В некоторой системе счисления записи десятичных чисел заканчиваются – как решать».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.