Радиус основания цилиндра равен M а его образующая

2016-02-28 16:01:09

Формулировка задачи: Радиус основания цилиндра равен M, а его образующая равна N. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное K. Найдите площадь этого сечения.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13 (Задачи по стереометрии).

Рассмотрим, как решаются подобные задачи на примере.

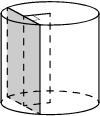
Пример задачи:

Радиус основания цилиндра равен 15, а его образующая равна 19. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 9. Найдите площадь этого сечения.

Решение:

Чтобы вычислить площадь сечения, нужно получить его стороны. Поскольку сечение параллельно оси цилиндра, одна из его сторон равна высоте (образующей) цилиндра, то есть равна 19.

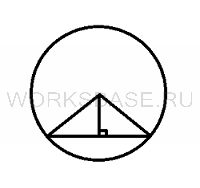
Чтобы найти другую сторону сечения, рассмотрим верхнее основание цилиндра, представляющее собой окружность. Нам известны радиус окружности и расстояние от центра окружности до сечения. Проведем 2 прямые из центра окружности до точек соприкосновения сечения с цилиндром (радиусы).

Получили 2 одинаковых прямоугольных треугольника. Рассмотрим один из них. В прямоугольном треугольнике известны гипотенуза и один катет. По теореме Пифагора можно получить другой катет:

√15² – 9² = √144 = 12

Таким образом, другая сторона сечения равна:

12 + 12 = 24

Осталось найти площадь сечения, перемножив его стороны:

S = 19 ⋅ 24 = 456

Ответ: 456

ЕГЭ база все задания ЕГЭ база задание 13

Поделитесь статьей с одноклассниками «Радиус основания цилиндра равен M а его образующая – как решать».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.