Найдите основание системы счисления, в которой выполнено сложение

2016-06-09 18:40:35

Формулировка задания: Найдите основание системы счисления, в которой выполнено сложение.

Задание входит в ЕГЭ по информатике для 11 класса под номером 16 (Кодирование чисел. Системы счисления).

Рассмотрим, как решаются подобные задания на примере.

Пример задания:

Найдите основание системы счисления, в которой выполнено сложение: 144 + 24 = 201.

Решение 1:

Для удобства запишем сложение в столбик:

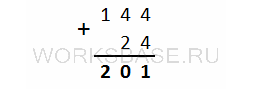
Стоит отметить, что система счисления не может быть меньше или равна 4, иначе цифры 4 в ней не будет. Значит, нужно начинать перебор с 5.

При сложении разряда единиц в результате получается меньшее число. Значит, было переполнение разряда:

4 + 4 = 11_x

8₁₀ = 11_x = 1 ⋅ x + 1

x + 1 = 8

x = 7

Можно предположить, что основание системы счисления равно 7. Убедимся в этом:

4 + 4 = 11₇ => 1

4 + 2 + 1 = 10₇ => 0

1 + 0 + 1 = 2₇ => 2

Решение 2:

Возьмем основание системы счисления за x и переведем каждое число в десятичную систему:

144_x = x² + 4x + 4

24_x = 2x + 4

201_x = 2x² + 1

Подставим числа в равенство и найдем, чему равен x:

x² + 4x + 4 + 2x + 4 = 2x² + 1

x² – 6x – 7 = 0

a = 1, b = -6, c = -7

D = (-6)² - 4 ⋅ 1 ⋅ (-7) = 36 + 28 = 64

D > 0 => имеется 2 различных корня

x1 = (6 + 8) / 2 = 7

x2 = (6 – 8) / 2 = -1

В качестве основания системы счисления подойдет только 7, так как второй корень отрицательный. Таким образом, основание системы счисления равно 7.

Ответ: 7

ЕГЭ все задания ЕГЭ задание 16

Поделитесь статьей с одноклассниками «Найдите основание системы счисления, в которой выполнено сложение – как решать».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.