Найдите длину высоты, опущенной на большую сторону параллелограмма

2016-02-06 18:35:55

Формулировка задачи: Стороны параллелограмма равны M и N. Высота, опущенная на меньшую сторону, равна K. Найдите длину высоты, опущенной на большую сторону параллелограмма.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 15 (Задачи по планиметрии).

Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.

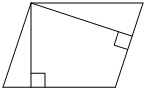
Пример задачи:

Стороны параллелограмма равны 10 и 12. Высота, опущенная на меньшую сторону, равна 6. Найдите длину высоты, опущенной на большую сторону параллелограмма.

Решение:

По условию задачи даны 2 стороны параллелограмма и одна из его высот. С помощью этих данных можно получить площадь параллелограмма:

S = 10 ⋅ 6 = 60

По второй стороне параллелограмма и площади можно получить искомую высоту:

H = 60 / 12 = 5

Ответ: 5

В общем виде решение данной задачи по планиметрии выглядит следующим образом:

S = a ⋅ h – площадь параллелограмма

H = S / b = a ⋅ h / b

где a – меньшая сторона, b – большая сторона, h – высота, опущенная на меньшую сторону, H – искомая высота.

Остается лишь подставить конкретные значения и подсчитать результат.

ЕГЭ база все задания ЕГЭ база задание 15

Поделитесь статьей с одноклассниками «Найдите длину высоты, опущенной на большую сторону параллелограмма – как решать».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.