Отрезки AB и CD пересекаются в точке N, которая является серединой каждой из них

2016-12-28 23:05:53

Формулировка задания: Отрезки AB и CD пересекаются в точке N, которая является серединой каждой из них. Найдите величину угла АСD, если угол СDВ равен 36°.

Решение:

Изобразим условие в виде рисунка:

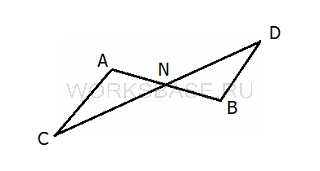
Мы видим, что:

∠ACD = ∠ACN

∠CDB = ∠BDN

Поэтому можно перейти от углов ∠ACD и ∠CDB к ∠ACN и ∠BDN.

Рассмотрим треугольники △ACN и △BDN:

AN = BN – по условию

CN = DN – по условию

∠ANC = ∠BND – так как вертикальные

Таким образом, треугольники △ACN и △BDN равны по 2 сторонам и углу между ними. Значит угол ∠ACD равен:

∠ACD = ∠ACN = ∠BDN = ∠CDB = 36°

Ответ: 36

Поделитесь статьей с одноклассниками «Отрезки AB и CD пересекаются в точке N, которая является серединой каждой из них – решение и ответ».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.