Основания трапеции равны a и b, отрезок с концами на боковых сторонах трапеции

2017-05-29 18:55:32

Формулировка задания: Основания трапеции равны a и b. Отрезок с концами на боковых сторонах трапеции, параллельный основаниям, разделяет трапецию на две трапеции, площади которых равны. Найти длину этого отрезка.

Решение:

Изобразим условие задачи на картинке:

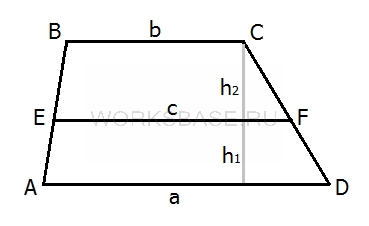
Площадь большой трапеции равна:

S_ABCD = (a + b)/2 ⋅ (h₁ + h₂)

Пусть длина отрезка, которую нужно найти, равна c. Площади малых трапеций, образованных в результате добавления отрезка EF в трапецию ABCD, равны:

S_EBCF = (b + c)/2 ⋅ h₂

S_AEFD = (a + c)/2 ⋅ h₁

Известно, что:

S_EBCF = S_AEFD

(b + c)/2 ⋅ h₂ = (a + c)/2 ⋅ h₁

Кроме этого площадь большой трапеции равна сумме площадей двух малых трапеций. А так как площади малых трапеций равны, площадь большой трапеции равна удвоенной площади любой из малых трапеций:

S_ABCD = S_EBCF + S_AEFD = 2S_AEFD

(a + b)/2 ⋅ (h₁ + h₂) = (a + c) ⋅ h₁

Получили систему из двух уравнений, которую нужно решить:

(b + c)/2 ⋅ h₂ = (a + c)/2 ⋅ h₁

(a + b)/2 ⋅ (h₁ + h₂) = (a + c) ⋅ h₁

Однако в ней получается много неизвестных: c, h₁ и h₂. Нужно избавиться от одного из неизвестных, чтобы система имела единственное решение. При этом мы знаем, что длины высот h₁ и h₂ зависят от длин оснований a и b, поэтому выполним следующую замену:

h₁ / h₂ = y

Теперь разделим оба уравнения на h₂, чтобы избавиться в них от h₁ и h₂:

(b + c)/2 ⋅ h₂ / h₂ = (a + c)/2 ⋅ h₁ / h₂

(a + b)/2 ⋅ (h₁ + h₂) / h₂ = (a + c) ⋅ h₁ / h₂

Получили систему из 2 уравнений с 2 неизвестными c и y:

b + c = (a + c) ⋅ y

(a + b)/2 ⋅ (y + 1) = (a + c) ⋅ y

Выразим из 1 уравнения y:

y = (b + c) / (a + c)

Подставим во 2 уравнение и решим его:

(a + b)/2 ⋅ ((b + c)/(a + c) + 1) = (a + c)⋅(b + c)/(a + c)

(a + b)/2 ⋅ ((b + c)/(a + c) + 1) = b + c

(a + b) ⋅ ((b + c)/(a + c) + 1) = 2 ⋅(b + c)

a ⋅(b + c)/(a + c) + b ⋅(b + c)/(a + c) + a + b = 2 ⋅(b + c)

a ⋅(b + c) + b ⋅(b + c) + a ⋅(a + c) + b ⋅(a + c) = 2 ⋅(b + c)⋅(a + c)

ab + ac + b² + bc + a² + ac + ab + bc = 2ab + 2bc + 2ac + 2c²

ac + bc + ac + bc – 2bc – 2ac – 2c² = 2ab – ab – ab – a² – b²

–2c² = – a² – b²

2c² = a² + b²

c² = (a² + b²)/2

c = √(a² + b²)/2

Таким образом, длина отрезка c была вычислена.

Ответ: √((a² + b²)/2)

Поделитесь статьей с одноклассниками «Основания трапеции равны a и b, отрезок с концами на боковых сторонах трапеции – решение и ответ».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.