На поверхности глобуса фломастером проведены параллели и меридианы

2016-01-23 15:27:29

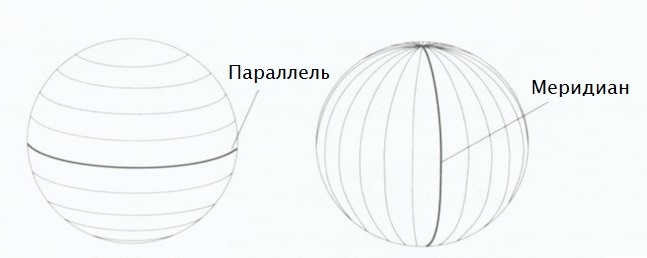
Формулировка задачи: На поверхности глобуса фломастером проведены A параллелей и B меридианов. На сколько частей проведённые линии разделили поверхность глобуса? Меридиан — это дуга окружности, соединяющая Северный и Южный полюсы. Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора.

Задача про глобус входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20 (Задачи на смекалку).

Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.

Пример задачи:

На поверхности глобуса фломастером проведены 12 параллелей и 22 меридиана. На сколько частей проведённые линии разделили поверхность глобуса?

Решение:

Чтобы правильно решить данную задачу, нужно понимать что такое параллели и меридианы. Главное отличие параллели от меридиана состоит в том, что параллель является окружностью, а меридиан - это дуга окружности. Именно поэтому одна параллель делит шар на 2 части, а один меридиан не может разделить шар на части.

Если мы проведем 2 параллели, то они разделят шар на 3 части, 3 параллели - на 4 части и т.д. Таким образом, если будет проведено 12 параллелей, они разделят шар на 13 частей.

Если мы проведем 2 меридиана, то они разделят шар на 2 части, 3 меридиана - на 3 части и т.д. Таким образом, если будет проведено 22 меридиана, они разделят шар на 22 части.

Осталось лишь провести параллели и меридианы на одном шаре и посчитать количество получившихся участков. Оно будет равно 13 ⋅ 22 = 286.

Ответ: 286

В общем виде решение данной задачи на смекалку выглядит следующим образом:

КОЛИЧЕСТВО ЧАСТЕЙ ГЛОБУСА = (A + 1) ⋅ B

где A - число проведенных параллелей, B - число проведенных меридианов. Остается лишь подставить числа в формулу и посчитать результат.

ЕГЭ база все задания ЕГЭ база задание 20

Поделитесь статьей с одноклассниками «На поверхности глобуса фломастером проведены параллели и меридианы – как решать».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.