Двускатную крышу дома, имеющего в основании прямоугольник

2016-02-20 12:47:41

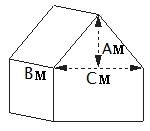
Формулировка задачи: Двускатную крышу дома, имеющего в основании прямоугольник, необходимо полностью покрыть рубероидом. Высота крыши равна A м, длины стен дома равны B м и C м. Найдите, сколько рубероида (в квадратных метрах) нужно для покрытия этой крыши, если скаты крыши равны.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 15 (Задачи по планиметрии).

Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.

Пример задачи:

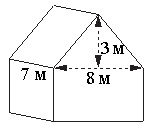
Двускатную крышу дома, имеющего в основании прямоугольник, необходимо полностью покрыть рубероидом. Высота крыши равна 3 м, длины стен дома равны 7 м и 8 м. Найдите, сколько рубероида (в квадратных метрах) нужно для покрытия этой крыши, если скаты крыши равны.

Решение:

Для решения данной задачи нужно найти площадь крыши, которую нужно покрыть рубероидом. Для этого нужно получить площади 2 прямоугольных скатов, длина которых известна и равна 7м, а ширину нужно найти.

Чтобы найти ширину ската, рассмотрим треугольник, образованный двускатной крышей и основанием дома. Поскольку скаты равны, треугольник является равнобедренным, следовательно, половина длины от его основания равна 4 метрам.

Теперь рассмотрим половину этого треугольника. Он является прямоугольным, поскольку одна из его сторон является высотой. У данного треугольника известны 2 катета, по ним можно найти гипотенузу, которая и является шириной 1 ската:

√4² + 3² = 5

Осталось лишь посчитать площадь одного ската и умножить его на 2, так как скаты равны:

5 ⋅ 7 = 35 м — площадь одного ската

35 ⋅ 2 = 70 м — площадь крыши

Ответ: 70

В общем виде решение данной задачи по планиметрии выглядит следующим образом:

ШИРИНА СКАТА = √A² + (C / 2)²

ПЛОЩАДЬ КРЫШИ = ШИРИНА СКАТА ⋅ B ⋅ 2

где A – высота крыши, B и C – длины стен дома (где B – длина крыши).

Остается лишь подставить конкретные значения и подсчитать результат.

ЕГЭ база все задания ЕГЭ база задание 15

Поделитесь статьей с одноклассниками «Двускатную крышу дома, имеющего в основании прямоугольник – как решать».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.