Задать множества A и B перечислением элементов

2016-12-01 19:00:56

Формулировка задания: Задать множества A и B перечислением элементов. Найти A⋃B, A⋂B, A∖B, B∖A, A×B, B×A.
A = {x ∈ R: |x + 2| = 3}, B = {x ∈ N: x / (x – 5) ≤ 0}.

Решение:

Решим первое уравнение и найдем все его корни:

|x + 2| = 3

x + 2 = 3 или x + 2 = –3

x = 1 или x = –5

Оба числа являются действительными (x ∈ R), поэтому множество A равно:

A = {–5, 1}

Решим второе неравенство: x может быть равен 0, и не может быть равен 5. Отметим эти точки на числовой прямой и определим, какие значение может принимать x:

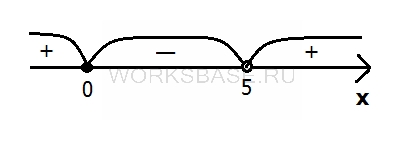
Таким образом, x ∈ [0; 5). Выберем из этого интервала только натуральные значения, так как x ∈ N, и получим второе множество B:

B = {1, 2, 3, 4}

Множества A и B заданы перечислением элементов. Осталось выполнить все необходимые операции над ними. Найдем объединение A⋃B:

A⋃B = {–5, 1} ⋃ {1, 2, 3, 4} = {–5, 1, 2, 3, 4}

Найдем пересечение A⋂B:

A⋂B = {–5, 1} ⋂ {1, 2, 3, 4} = {1}

Найдем разности A∖B и B∖A:

A∖B = {–5, 1} ∖ {1, 2, 3, 4} = {–5}

B∖A = {1, 2, 3, 4} ∖ {–5, 1} = {2, 3, 4}

Найдем декартовые произведения A×B и B×A:

A×B = {–5, 1} × {1, 2, 3, 4} = {(–5, 1), (–5, 2), (–5, 3), (–5, 4), (1, 1), (1, 2), (1, 3), (1, 4)}

B×A = {1, 2, 3, 4} × {–5, 1} = {(1, –5), (1, 1), (2, –5), (2, 1), (3, –5), (3, 1), (4, –5), (4, 1)}

Поделитесь статьей с одноклассниками «Задать множества A и B перечислением элементов – решение и ответ».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.