Докажите, что дроби 1000/1993 и 993/1993 имеют одинаковую длину периодов

Решение:

Обратим внимание, что сумма дробей равна единице:

Значит, если нам известно точное значение первой дроби, значение второй дроби можно получить, вычитая из единицы значение первой дроби.

Рассмотрим это на примере. Пусть значение первой дроби равно 0,486721. Заполняем дробную часть единицы нулями по количеству цифр в дробной части первого числа:

Начнем выполнять поразрядное вычитание. Чтобы из нуля вычесть 1, нужно занять единицу из старшего разряда. Однако он тоже равен нулю. Значит, нужно занять эту единицу из следующего разряда и т.д. В результате, мы получаем следующее:

Таким образом, фактически мы вычитаем значение первой дроби не из единицы, а из числа 0,(9). Теперь выполняем само вычитание:

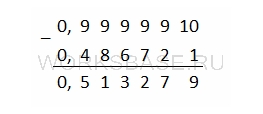
Заметим, что каждая цифра второй дроби будет зависеть от цифры первой дроби в соответствующем разряде: если в первой дроби 1, то во второй будет 8, если в первой дроби 2, то во второй будет 7 и т.д. Исключение составляет только самый младший разряд, однако в числе с дробным периодом погрешность будет настолько мала, что ею можно пренебречь.

Следовательно, если у первой дроби есть период, у второй дроби будет период той же длины, только цифры в них будут отличаться.

Ответ: дроби имеют одинаковую длину периодов