Наибольший общий делитель
Наибольший общий делитель чисел – это наибольшее число, на которое делятся все заданные числа.
Алгоритм поиска НОД
Вычисление НОД похоже на поиск НОК. Чтобы найти наибольший общий делитель, нужно использовать следующий алгоритм:
- Разложить все числа на простые множители, используя признаки делимости чисел.
- Найти совпадающие множители во всех числах и выписать их.
- Перемножить совпадающие множители.
Если среди множителей чисел не были найдены одинаковые, числа являются взаимно простыми.
Примеры поиска наибольшего общего делителя
Рассмотрим, как найти НОД с помощью алгоритма на нескольких примерах.
Пример 1:
Найдите наибольший общий делитель чисел 420 и 990.
Решение:
Разложим оба числа на простые множители:
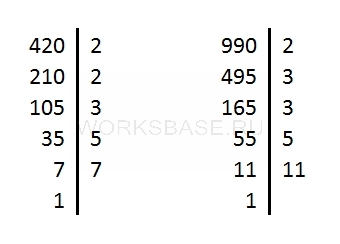
Получили, что:
420 = 2 ⋅ 2 ⋅ 3 ⋅ 5 ⋅ 7
990 = 2 ⋅ 3 ⋅ 3 ⋅ 5 ⋅ 11
Выпишем все совпадающие множители для обоих чисел и перемножим их:
НОД = 2 ⋅ 3 ⋅ 5 = 30
Ответ: 30
Пример 2:
Найдите наибольший общий делитель чисел 588 и 1820.
Решение:
Разложим оба числа на простые множители:

Получили, что:
588 = 2 ⋅ 2 ⋅ 3 ⋅ 7 ⋅ 7
1820 = 2 ⋅ 2 ⋅ 5 ⋅ 7 ⋅ 13
Выпишем все совпадающие множители для обоих чисел и перемножим их:
НОД = 2 ⋅ 2 ⋅ 7 = 28
Пример 3:
Найдите наибольший общий делитель чисел 1000 и 3267.
Решение:
Разложим оба числа на простые множители:
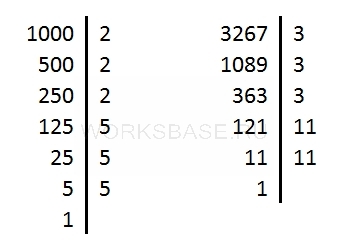
Получили, что:
1000 = 2 ⋅ 2 ⋅ 2 ⋅ 5 ⋅ 5 ⋅ 5
3267 = 3 ⋅ 3 ⋅ 3 ⋅ 11 ⋅ 11
Совпадающих множителей у этих 2 чисел нет, поэтому они являются взаимно простыми, то есть
НОД = 1
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.