В бак имеющий форму правильной четырёхугольной призмы со стороной основания

2016-05-02 19:48:30

Формулировка задачи: В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной K см, налита жидкость. Для того чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если уровень жидкости в баке поднялся на N см. Ответ дайте в кубических сантиметрах.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13 (Задачи по стереометрии).

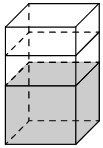
Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.

Пример задачи:

В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 20 см, налита жидкость. Для того чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если уровень жидкости в баке поднялся на 20 см. Ответ дайте в кубических сантиметрах.

Решение:

В основании правильной четырехугольной призмы лежит квадрат со стороной 20 см. Поэтому его площадь будет равна:

20 ⋅ 20 = 400 см²

При погружении детали в жидкость ее уровень поднялся на 20 см. Получается, что объем жидкости изменился на:

400 ⋅ 20 = 8000 см³

Объем детали равен объему жидкости, который она вытеснила. Таким образом, объем детали равен 8000 куб. см.

Ответ: 8000

В общем виде решение данной задачи по стереометрии выглядит следующим образом:

ОБЪЕМ ДЕТАЛИ В КУБ. СМ = K² ⋅ N

где N – высота, на которую поднялся уровень уровень жидкости в баке, K – сторона основания правильной четырехугольной призмы.

Остается лишь подставить значения и вычислить результат.

ЕГЭ база все задания ЕГЭ база задание 13

Поделитесь статьей с одноклассниками «В бак имеющий форму правильной четырёхугольной призмы со стороной основания – как решать».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.