Найдите значение алгебраического выражения

2017-02-26 20:43:07

Формулировка задачи: Найдите значение алгебраического выражения.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 5 (Вычисления и преобразования).

Рассмотрим, как решаются подобные задачи на примерах.

Пример задачи 1:

Найдите значение выражения:

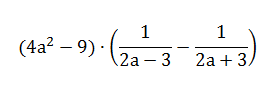
Решение:

Приведем разность в скобках к общему знаменателю:

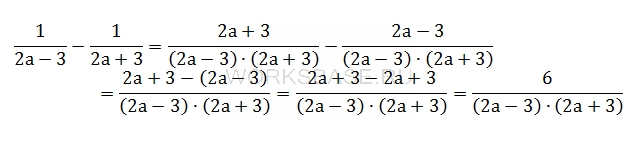
Преобразуем первый множитель по формуле разности квадратов и сократим получившуюся дробь:

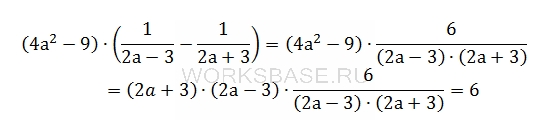
Ответ: 6

Пример задачи 2:

Найдите значение выражения

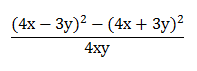
Решение:

Преобразуем числитель по формуле разности квадратов, приведем подобные и сократим дробь:

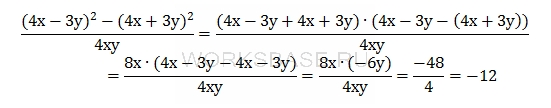
Ответ: -12

Пример задачи 3:

Найдите значение выражения 2x + y + 6z, если 4x + y = 5, а 12z + y = 7.

Решение:

Легко заметить, что если мы сложим 2 приведенных равенства, то получим удвоенное значение выражения, которое нужно найти:

4x + y + 12z + y = 4x + 2y + 12z = 5 + 7 = 12

Поэтому нам достаточно разделить получившееся значение пополам:

4x + 2y + 12z = 12

2x + y + 6z = 6

Ответ: 6

Пример задачи 4:

Найдите значение выражения 5(p(2x) – 2p(x + 5)), если p(x) = x – 10.

Решение:

Найдем, чему равно p(2x), для этого в функцию p(x) подставим в качестве аргумента 2x:

p(2x) = 2x – 10

Найдем, чему равно p(x + 5), для этого в функцию p(x) подставим в качестве аргумента x + 5:

p(x + 5) = x + 5 – 10 = x – 5

Подставим полученные значения в выражение и вычислим его значение:

5(p(2x) – 2p(x + 5)) = 5 ⋅ (2x – 10 – 2 ⋅ (x – 5)) = 5 ⋅ (2x – 10 – 2x + 10) = 5 ⋅ 0 = 0

Ответ: 0

Пример задачи 5:

Найдите значение выражения (√10 – 2√3)(√10 + 2√3)

Решение:

Преобразуем выражение по формуле разности квадратов, чтобы избавиться от корней, и вычислим значение выражения:

(√10 – 2√3)(√10 + 2√3) = (√10)² – (2√3)² = 10 – 4 ⋅ 3 = 10 – 12 = -2

Ответ: -2

Пример задачи 6:

Найдите значение выражения

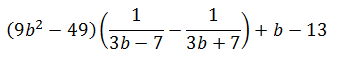
при b = 345

Решение:

Приведем разность в скобках к общему знаменателю и упростим числитель:

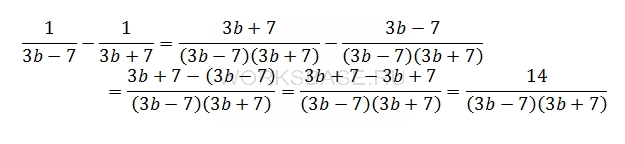
Преобразуем первый множитель по формуле разности квадратов и заменим упрощенную разность:

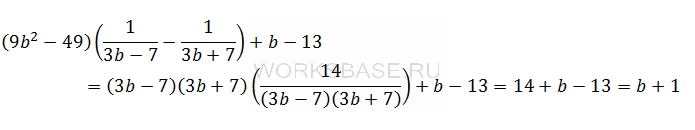
Осталось подставить значение b и вычислить результат:

b + 1 = 345 + 1 = 346

Ответ: 346

Пример задачи 7:

Найдите

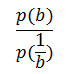
если

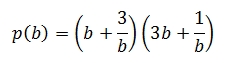
при b ≠ 0

Решение:

Найдем значение p(1/b), для этого в функцию p(b) подставим в качестве аргумента 1/b:

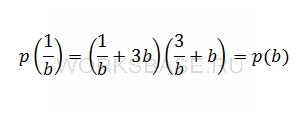
Поскольку p(1/b) равно p(b), частное от их деления будет равно 1:

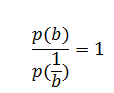
Ответ: 1

Пример задачи 8:

Найдите p(x) + p(6 – x), если

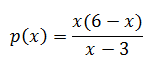
при x ≠ 3

Решение:

Найдем значение p(6 – x), для этого в функцию p(x) подставим в качестве аргумента 6 – x:

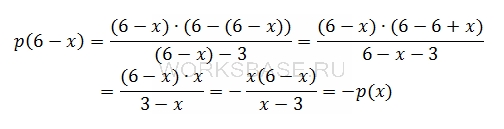
Тогда значение выражения равно:

p(x) + p(6 – x) = p(x) – p(x) = 0

Ответ: 0

Пример задачи 9:

Найдите a/b, если

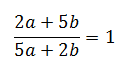
Решение:

Разделим и числитель и знаменатель на b:

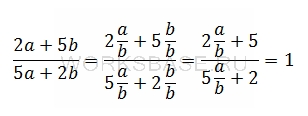
Таким образом среди неизвестных осталась только дробь a/b, которую и нужно найти. Вычислим ее значение из равенства:

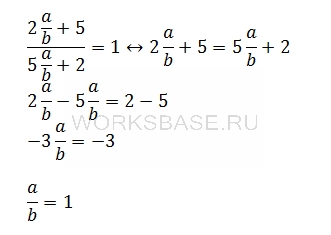
Ответ: 1

Пример задачи 10:

Найдите

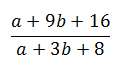
если a/b = 3.

Решение:

Разделим числитель и знаменатель на b и заменим a/b на 3, после чего упростим выражение:

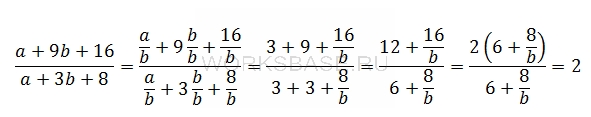
Ответ: 2

ЕГЭ база все задания ЕГЭ база задание 5

Поделитесь статьей с одноклассниками «Найдите значение алгебраического выражения – как решать».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.