Найти наибольшее и наименьшее значения суммы

2016-07-25 19:55:47

Формулировка задания: Найти наибольшее и наименьшее значения суммы 2x² + 3y²
при условиях x + y = 2, x ≥ 0, y ≥ 0.

Решение:

Для начала определим, в каких интервалах лежат значения x и y, используя исходные условия:

x + y = 2 ⇒ y = 2 – x

x ≥ 0

y ≥ 0

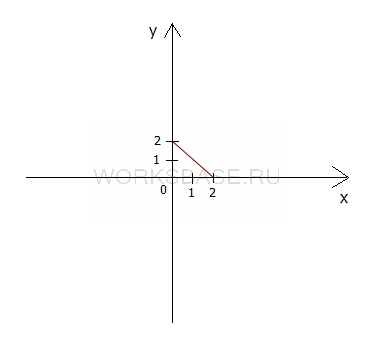
Получается, что:

0 ≤ x ≤ 2

0 ≤ y ≤ 2

Рассмотрим функцию:

z = 2x² + 3y²

Подставим в функцию вместо y выражение 2 – x, полученное из условия:

z = 2x² + 3 ⋅ (2 – x)² = 2x² + 3 ⋅ (4 – 4x + x²) = 2x² + 12 – 12x + 3x² = 5x² – 12x + 12

Найдем ее производную:

z' = (5x² – 12x + 12)' = 10x – 12

Приравняем производную к нулю, чтобы получить точки экстремума:

10x – 12 = 0

10x = 12

x = 1,2

1,2 принадлежит интервалу 0 ≤ x ≤ 2. Функция z является параболой, ветви которой направлены вверх (так как a = 5 > 0), значит 1,2 – точка минимума.

Найдем значения функции в точке минимума и на концах отрезка (в точках 0 и 2):

z(1,2) = 5 ⋅ 1,2² – 12 ⋅ 1,2 + 12 = 4,8

z(0) = 5 ⋅ 0² – 12 ⋅ 0 + 12 = 12

z(2) = 5 ⋅ 2² – 12 ⋅ 2 + 12 = 8

Таким образом, наибольшее значение функции равно 12, а наименьшее значение функции равно 4,8.

Ответ: 12 и 4,8

Поделитесь статьей с одноклассниками «Найти наибольшее и наименьшее значения суммы – решение и ответ».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.